mise à jour : 31-03-2010
cinet.chim
III. Cinétique des réactions élémentaires
complément
dy/dt = p y + q y 2 (Q1)
L'intégration de l'équation avec terme constant se ferait suivant une méthode analogue. Nous nous sommes limités ici au cas qui nous intéresse en cinétique.
Il s'agit d'intégrer l'équation (Q1) entre 0 et t (y0 et y) :
∫y0→y dy / (py + qy2) = ∫0→t dt (a)
Afin de la réduire en éléments plus simples, nous cherchons à déterminer P et Q, tels que :
1 / (py + qy2) = 1 / [ y (p + qy) ] ≡ P / y + Q / (p + qy) ∀ y
1 / [ y (p + qy) ] ≡ [ P(p + qy) + Qy ] / [ y (p + qy) ]
on doit donc avoir :
P(p + qy) + Qy = Pp + (Pq + Q)y = 1 ∀ y
soit
Pp = 1 et Pq + Q = 0
d'où l'on tire
P = 1 / p
Q = − q / p
L'équation (a) peut alors s'écrire :
∫y0→y dy / y + q ∫y0→y dy / (p + qy) = p ∫0→t dt (b)
qui s'intègre immédiatement :
ln (y / y0) − ln [(p + qy) / (p + qy0)] = p t
[ y (p + qy0) ] / [ y0 (p + qy) ] = e pt (c)
et, en arrangeant la relation (c), on obtient la fonction intégrée générale :
y = py0 / [ (p + qy0) e −pt −qy0 ] (Q2)
L'équation (Q1), en tant que telle, n'est pas invariante de type 2. En effet, si on change y en Y = αy et t en θ = t/α, on obtient l'équation :
dY/dθ = α2 dy/dt = α2 (pY/α + qY2/α2) = αpY + qY2
qui est différente de (Q1).
Cependant, pour ce qui nous concerne, il s'agit en fait d'une équation commune à plusieurs variables, liées par un système d'équations différentielles. Il en résulte que le paramètre p est en réalité proportionnel aux concentrations initiales. Le système d'équation est bien alors invariant de type 2. Ce point est discuté dans chaque cas particulier.
Cette équation générale s'applique à au moins sept types de réactions, élémentaires ou composées, avec des valeurs des constantes p, q et y0 spécifiques à chacune d'entre elles. Ces réactions ne sont pas toutes monovariables, il s'ensuit que l'équation Q1 ne s'applique qu'aux espèces indiquées pour chaque cas.
La conséquence la plus importante est que toutes ces réactions ont des cinétiques dépendant seulement des 3 paramètres p, q et y0. Cela signifie qu'en présence d'une courbe cinétique expérimentale émanant de l'une de ces réactions, seuls ces 3 paramètres peuvent être déterminés. Il peut alors être difficile, sans autre données, de remonter jusqu'au vrai mécanisme réactionnel. On pourra trouver une discussion plus approfondie en fonction des valeurs de ces paramètres dans :
Reversible, mixed first- and second-order and autocatalytic
reactions as particular cases of a single kinetic rate law.
D. Lavabre, V. Pimienta, G. Levy and J.C. Micheau.
The Journal of Physical Chemistry, vol. 97, pp
5321-5326, 1993
1. bimoléculaire générale :
A + B → P k
y = A ; y0 = A0
p = −k(A0−B0)
q = −k
monovariable : A, B, P de la forme Q1
2. monomoléculaire et bimoléculaire pure parallèles :
A → B k0
2 A → C k1
y = A ; y0 = A0
p = −k0
q = −2k1
2 variables : seul A de la forme Q1
3.monomoléculaire et autocatalyse bimoléculaire parallèles :
A → B k0
A + B → 2 B k1
y = A ; y0 = A0 ; B0 = 0
p = −(k0+k1A0)
q = k1
monovariable : A et B de la forme Q1
Ce cas s'apparente à l'autocalyse bimoléculaire seule présentée dans le cours, il en est une variante permettant à la réaction de démarrer en l'absence d'autocatalyseur (B0 = 0).
4. bimoléculaire réversible :
A + B ⇄ C + D k0, k1
y = E = A−Ae ; y0 = A0−Ae
p = −[ k0 (Be+Ae) + k1 (Ce+De) ]
q = k1−k0
monovariable : A, B, C, D de la forme Q1
5. bimoléculaire contre monomoléculaire :
A + B ⇄ C k0, k1
y = E = A−Ae ; y0 = A0−Ae
p = −[ k0 (Be+Ae) + k1]
q = −k0
monovariable : A, B, C de la forme Q1
6. monomolécualire et autocatalyse bimoléculaire réversibles parallèles :
A ⇄ B k0, k1
A + B ⇄ 2 B k2, k3
y = E = A−Ae = Be−B ; y0 = E0 = A0−Ae
p = −[ k0 + k1 + (A0 + B0)(k2 + 2k3) −2(k2 + k3)Ae ]
q = k2 + k3
monovariable : A, B de la forme Q1
7. processus de croissance et auto inhibition :
A (+ S) → 2 A k0 (r1)
2 A → B k1 (r2)
La réaction (r1) représente la formation autocatalytique de A en présence d'un substrat S (sa nourriture) et la réaction (r2) son auto inhibition, B désignant une espèce morte. L'ensemble de ces deux réactions se met sous la forme Q1 pour A, si l'on suppose S illimité et constant (r0 = (k'S)A = k0A). L'équation cinétique est donc :
dA/dt = A(k0 −2k1A)
y = A ; y0 = A0
p = k0
q = −2k1
2 variables : seul A, avec S constant, est de la forme Q1.
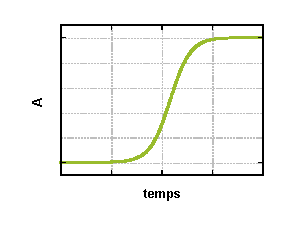
La forme caractéristique de cette fonction, appelée fonction logistique, est montrée ci-dessus. A atteint un état stationnaire, que l'on peut faire varier, par exemple en changeant la concentration S (nourriture).
Cette forme rappelle celle de l'autocatalyse, en sens inverse, c'est-à-dire celle du produit de la réaction. Mais il s'agit d'un processus totalement différent : la réaction (r 1) correspond à une croissance exponentielle (à coefficient positif, explosive), elle est limitée par l'auto-inhibition de la réaction (r 2). A l'inverse, l'autocatalyse est un processus d'ordre 1 (à coefficient négatif) accéléré par le produit.