mise à jour :31-03-2010 cinet.chim
VI.1 Ajustement d'une courbe expérimentale
(tutoriel Sa)

Exercice 16
Contact : cinet.chim@orange.fr
Vous trouverez une présentation générale des problèmes d'optimisation dans le complément :
| 1. Données
expérimentales sans bruit expon_0pc.exp |
2. Données
expérimentales avec 2% de bruit expon_2pc.exp |
| 3. Données
expérimentales avec 10% de bruit expon_10pc.exp |
4. Rejet du
modèle non_expon_2pc.exp non_expon_10pc.exp |
Supposons que nous disposions de différents lots de données cinétiques, c'est-à-dire des valeurs d'une certaine grandeur, Y, proportionnelle aux concentrations, mesurées à certains instants d'une réaction, t0, t1, etc.. Nous nous proposons simplement de déterminer si chacune de ces courbes cinétiques peut-être ajustée par une exponentielle, et, si oui, d'en déterminer la constante de vitesse.
Si Y0 désigne la valeur initiale et Y∞ la valeur à l'équilibre, on veut donc déterminer si ces données peuvent être ajustées avec la fonction
Y = Y∞ + (Y0 − Y∞) e−kt (a)
qui dépend des trois paramètres Y0, Y∞ et k. Nous supposerons que Y0 est connu avec précision et que les deux paramètres inconnus, à ajuster, sont donc Y∞ et k.
La première chose à faire est donc d'écrire un programme permettant de calculer les valeurs de la fonction (a), afin de pouvoir les comparer aux valeurs expérimentales.
Lors de l'étude des réactions monomoléculaires, nous avons déjà programmé
cette fonction dans le cas où Y représente
l'absorbance UV-Visible (voir Exercice 1,
monomol_2.cpp). L'exponentielle y était calculée par intégration numérique.
Nous utiliserons ici une version algébrique équivalente, qui ne préjuge en rien
de la nature réelle de Y et valable même si la
réaction n'est pas totale , dans laquelle
p[0] = k
p[1] = Y0
p[2] = Y∞
soit :
void fappel()
{
for (int i = 0; i < npt; ++i)
ca[0][i] = p[2] + (p[1]-p[2])*exp(-p[0]*ind[i]);
}
Noter que dans cette version, la valeur initiale (à t = 0) est
donnée par le paramètre p[1], et non par la valeur de
ca[0][0].
Compilez Sa avec expon.cpp puis exécutez-le.
Chargez le fichier expon.sac, qui contient les paramètres et les variables correspondants, mais à des valeurs quelconques.
Nous donnons ci-dessous de façon très détaillée les opérations à effectuer pour réaliser l'ajustement.
A - Préciser quelle est la variable
expérimentale, ou observée. Ici, il n'y a pas le choix
puisqu'il n'y a qu'une seule variable, ca[0][]. Encore faut-il
indiquer que c'est elle la variable expérimentale, en cochant la case
obs correspondante, afin que Sa établisse le lien entre le
fichier expérimental et cette variable :
Ecran 1. Onglet Variables de la fenêtre Infos :
cocher la case obs de la (des) variable(s)
correspondant au fichier de données expérimentales, avant la lecture de
ce dernier. Comme déjà vu (exercice 1), cela provoquera, d'autre part,
le tracé automatique de cette variable au terme de tout calcul (simulation ou
optimisation).
La valeur initiale de Y (ca[0][0]) peut, dans ce cas
particulier, être quelconque puisqu'elle sera donnée en réalité par
p[1].
B - Lire le fichier expérimental.
Téléchargez préalablement le fichier expon_0pc.exp et enregistrez-le dans votre dossier de travail (W.D.). Ce fichier, en mode texte, ne contient strictement que des données numériques (pas d'entête de colonnes). La première colonne contient les temps. L'intervalle entre deux temps successifs est ici constant, mais ce n'est pas obligatoire. La deuxième colonne contient les valeurs expérimentales correspondantes. Dans la pratique, c'est vous qui devrez construire ce type de fichier, à partir de données expérimentales réelles. L'extension .exp n'est pas obligatoire (vous pouvez utiliser .txt ou ce que vous voulez).
Cliquez sur l'onglet Données exp. puis sur Lire et sélectionnez le fichiez ci-dessus. L'onglet apparaît alors comme sur l'écran ci-dessous :
Ecran 2. Onglet Données exp. après lecture du fichier expérimental (expon_0pc.exp). Noter que n_exp = 1 (initialisé dans la fonction Identification de expon.cpp). La case Protégé est cochée par défaut : cela interdit de modifier accidentellement le fichier expérimental (précieux en général), mais il est possible de le faire, depuis Sa, en dé-cochant cette case. Cochez la case Actif : données expérimentales et données calculées seront alors tracées simultanément en fin de tout calcul.
Noter l'apparition, à la lecture d'un fichier expérimental, d'un nouvel onglet nommé Pondération (marqué en bleu), qui permet de pondérer les données expérimentales. Nous ne nous en occuperons pas pour l'instant.
C - Estimer grossièrement les valeurs des paramètres.
Si les valeurs de départ des paramètres sont trop éloignées de leurs valeurs réelles, la procédure d'ajustement peut rester piégée dans un faux minimum, ou minimum local (voir Optimisation ). Il est donc capital de les estimer manuellement, autant qu'il se peut. Toutes les méthodes peuvent être utiles : connaissance préalable d'ordre de grandeur de certains paramètres, estimation graphique, etc.
Les données du fichier expon_0pc.exp ont pour représentation graphique la figure 1 :
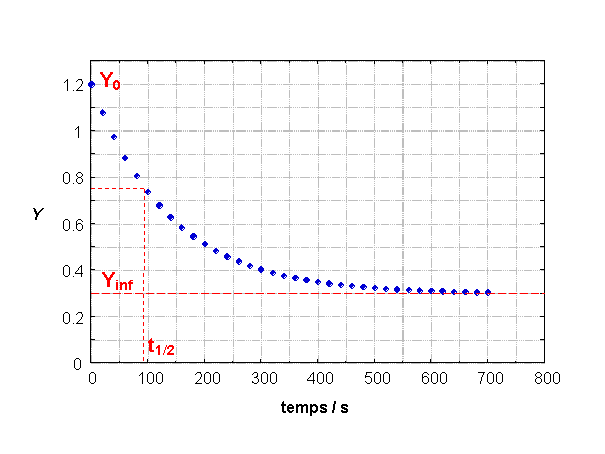
On peut y estimer :
Y0 = 1.2 = p[1] , que
l'on considérera comme sa valeur exacte, non ajustable.
Y∞ ≈ 0.3 =
p[2]
t1/2 ≈ 90 s
on en déduit k ≈ ln 2 / t1/2 ≈
8×10−3 (s−1) = p[0]
Nous n'indiquons pas d'unités pour Y, qui peut être n'importe quelle grandeur.
On affectera donc ces valeurs aux paramètres pour démarrer l'ajustement.
D - Préciser les paramètres ajustables.
Les valeurs de départ des paramètres étant fixées, il faut préciser quels paramètres doivent être ajustés, en cliquant deux fois sur la case mode correspondante :
Ecran 3. Choix des paramètres ajustables.
En faisant cela, vous remarquerez que des zéros apparaissent dans les cases min et max. C'est sans importance pour l'instant.
Il est possible également de désigner des valeurs initiales des variables comme paramètres ajustables (onglet Variables).
A ce stade, il est conseillé de sauver le fichier de paramètres de départ, par exemple sous le nom expon_depart.sac.
E - Vérifier la situation de départ.
Si vous lancez maintenant une simulation, les données expérimentales étant marquées comme actif, vous obtiendrez leur tracé, superposé à celui des données calculées. Cela vous permet d'évaluer visuellement votre position de départ, et éventuellement de la rectifier.
Vous pouvez même essayer d'effectuer un ajustement manuel, par essais successifs. Vous pouvez apprécier la qualité de l'ajustement graphiquement, mais aussi numériquement. Pour cela, au lieu de lancer une simple simulation, effectuez une Simulation + calcul de l'erreur, en pressant le bouton indiqué ci-dessous :
Ecran 4. Fenêtre principale :
lancement d'une Simulation + calcul de l'erreur.
En plus du tracé superposé précédent, ce mode de calcul se termine par l'ouverture d'une fenêtre, comme dans le cas de l'ajustement (voir écran 5), qui indique la valeur de l'erreur résiduelle.
F - Ajustement.
Dans la fenêtre principale, enfoncez le bouton Opt, immédiatement à droite de Sim. Sa travaillera dès lors en mode d'optimisation, ou ajustement, des paramètres marqués comme ajustables, c'est-à-dire qu'il cherchera automatiquement un jeu de ces paramètres qui minimise l'erreur résiduelle.
Dans l'onglet Général de la fenêtre Infos, regardez le panneau Optimisation. Il vous indique le nombre de paramètres marqués ajustables et vous permet de préciser deux paramètres d'optimisation :
- la précision : l'optimisation s'arrêtera lorsque tous les paramètres ajustables ne varieront plus que d'une valeur (relative) inférieure à la précision. La valeur 1/100 convient dans la plupart des problèmes, mais il peut arriver qu'on ait besoin de la changer.
- le résiduel attendu : les données expérimentales sont toujours bruitées, de sorte que, même parfaitement ajustées avec le modèle qui convient, il restera une certaine erreur résiduelle correspondant à leur dispersion. C'est le résiduel attendu, qui dépend significativement du type de données considérées. L'optimisation s'arrêtera également lorsque l'erreur résiduelle deviendra égale au résiduel attendu, qui doit donc être convenablement réglé . Laissez pour l'instant la valeur de 10−6, qui conviendra pour cet exemple.
L'ordre de grandeur de l'erreur résiduelle dépend bien sûr de la qualité de l'ajustement, mais aussi de l'ordre de grandeur des données ajustées et de leur précision. Ainsi, par exemple, si les données ajustées sont des concentrations de l'ordre de 10−5 ou 10−6 mol.L−1,avec 2 ou 3 chiffres significatifs, l'erreur résiduelle pourra être de l'ordre de 10−12 ou 10−13, tandis que pour des données d'absorption, de l'ordre de 1 et dont la précision est courament de l'ordre de 10−3, elle sera autour de 10−6 (voir l'expression de l'erreur résiduelle).)
Dans le mode optimisation, lancez un calcul (bouton habituel).
Il vous est demandé si vous voulez une estimation automatique de l'erreur ; entendez par là le résiduel attendu.. Répondez Non.
La fenêtre Ordre des directions initiales s'ouvre. Il s'agit de l'ordre dans lequel les paramètres seront modifiés, dans la phase initiale de l'optimisation. La première ligne indique les numéros affectés aux paramètres ajustables par l'optimisateur. Il est possible de modifier aléatoirement cet ordre à l'aide du bouton Brouiller. Cela peut être très utile lorsqu'il y a plus de paramètres ajustables, mais n'a guère d'intérêt ici. Cette fenêtre permet également d'annuler le lancement de l'optimisation ; cela ne sera en général plus possible après.
Appuyez sur OK pour continuer.
L'optimisation est ici extrêmement rapide et vous aurez vraisemblablement un résultat immédiat, disponible sous différentes formes :
- le graphique : le tracé superposé des données calculées, après ajustement des paramètres, et des données expérimentales. Il permet d'apprécier visuellement la qualité de l'ajustement.
- la fenêtre Optimisation :
Ecran 5. Fenêtre Optimisation.
- le 1er bouton en haut à gauche permet de revenir aux valeurs
de départ (par défaut les valeurs ajustées remplacent celles-ci).
- le 2me bouton permet d'interrompre l'optimisation, mais cela
ne sera effectif qu'à l'itération suivante (voir ci-dessous)
- Méthode : va04a, c'est la méthode d'optimisation sélectionnée
lorsque le bouton Opt est enfoncé (recommandé d'une manière
générale).
- Appels : nombre de fois que la fonction fappel a
été appelée au cours d'essais de l'optimisation. Il peut atteindre des valeurs
élevées.
- Itérations : nombre d'appels réussis, c'est-à-dire ayant permis
de diminuer l'erreur résiduelle.
- Terminaison : indique si le calcul s'est terminé normalement ou
a été avorté. Vérifiez toujours cette indication : Si le calcul ne s'est pas
déroulé "normalement", les résultats risquent d'être erronés.
- Le résultat proprement dit : valeur après optimisation de l'erreur
résiduelle et des paramètres.
Noter que ces valeurs sont données avec le nombre de chiffres interne au
calcul, car il est parfois utile de voir à quel niveau de précision se situent
les variations pendant l'optimisation. Cela n'a évidemment rien à voir avec
leur précision en tant que résultat.
L'erreur résiduelle obtenue ici est très petite. C'est normal : les données expérimentales du fichier expon_0pc.exp ont été en réalité simulées avec la fonction (a), 0% de bruit, k = 7.2×10−3 s−1 et Y∞ = 0.3 .
- le fichier .sao (sa o-ptimisation) : un fichier de même nom que le fichier .sac courant, avec l'extension .sao, est automatiquement enregistré. Il contient les paramètres optimisés. Vous pouvez le visualiser directement par le bouton "o" de la fenêtre principale, et le sauver éventuellement sous un autre nom. Noter que les paramètres courants, dans l'onglet Paramètres, sont également les paramètres optimisés (sauf si vous avez appuyé sur le bouton de retour aux paramètres de départ).
- le fichier .sar (sa r-ésumé d'optimisation) : ce fichier, également de même nom que le fichier .sac courant, et directement accessible par le bouton "r", contient le résumé, l'historique, de l'optimisation. Il peut être très instructif de le consulter.
- le fichier .sad : ce fichier est créé automatiquement comme dans le cas d'une simple simulation, mais cette fois il rassemble dans un même fichier les données calculées et expérimentales, ce qui peut être pratique pour les présenter graphiquement.
Avant de passer à des situations plus réalistes, livrez-vous à une petite
expérience :
mettez
k = 5×10−3 s−1 ;
Y∞ = 10−6
et faites une simple simulation.
Le résultat n'est certes pas brillant, mais, toutefois, on peut dire qu'on n'est pas si loin du but : les courbes simulée et expérimentale sont dans les mêmes échelles de grandeur.
Lancez maintenant une optimisation. Vous aurez vraisemblablement un message d'erreur "Overflow". Cliquez sur OK, et regardez la fenêtre d'optimisation : Appel est à quelque chose comme 1026, et Itération à 0, ce qui veut dire que l'optimisateur n'a jamais réussi à diminuer l'erreur résiduelle au cours de ces 1026 appels (raison de l'Overflow), et le message de Terminaison est "L'erreur ne varie plus"... en fait, elle n'a jamais varié !
Cette expérience, dans une situation pourtant extrêmement facile, montre l'absolue nécessité de démarrer une optimisation avec des paramètres de départ réalistes.
Les paramètres ajustables ne doivent jamais être mis à zéro, car l'optimisateur serait alors dans l'impossibilité de les faire varier. C'est pourquoi nous avons mis Y∞ = 10−6, ci-dessus.
Ce fichier, comme le précédent, a été réalisé par simulation de l'équation (a) et avec les mêmes paramètres, mais il lui a été ajouté 2% de bruit, ce qui correspond à une situation moyenne fréquente.
On peut donc démarrer l'optimisation avec les paramètres estimés dans la première partie.
Réalisez l'optimisation.
L'erreur résiduelle doit être cette fois de l'ordre de 2.8×10−5, soit environ 1010 fois plus qu'avec les données non bruitées. Cela est dû à la présence du bruit et ne signifie pas, en soi, que l'ajustement soit bon ou mauvais. Le graphique montre d'ailleurs qu'il est excellent, et les paramètres ajustés, bien que légèrement moins précis, sont corrects.
Pour apprécier la qualité de l'ajustement, vous disposez de deux outils supplémentaires :
1 - Dans la fenêtre Optimisation, appuyez sur le bouton Tracé des résiduels. Cela affiche la fenêtre Résiduel. Dans la colonne de gauche, sélectionnez la variable Y (en fait il n'y a qu'elle dans ce cas) pour obtenir le tracé de son résiduel, en fonction de la variable indépendante. L'erreur résiduelle est une estimation globale, le tracé des résiduels en précise la forme, en fonction de la variable indépendante. Un ajustement correct se caractérise par une répartition aléatoire du résiduel (Fig. 2-a). Si ce dernier présente des zones systématiquement positives tandis que d'autres sont négatives (Fig. 2-b), cela signifie soit que l'optimisation s'est arrêtée dans un minimum local, soit que le modèle n'est pas tout à fait correct.
Fig. 2-a Résiduel correct, réparti aléatoirement (obtenu lors de l'ajustement de expon_2pc.exp)
Fig. 2-b Résiduel défectueux : zones positives et zones négatives (obtenu avec les mêmes données expérimentales et un modèle incorrect)
Ce tracé montre en réalité la même chose que le tracé superposé des données calculées et expérimentales, mais il est en général plus clair.
Noter qu'une "répartition aléatoire du résiduel" suppose un nombre relativement important de données. Si l'on dispose de très peu de points (disons moins d'une quinzaine pour fixer les idées), il est évident que les défauts signalés ci-dessus ne peuvent pas être considérés comme très significatifs.
N'oubliez pas de sélectionner, dans la colonne de gauche de la fenêtre Résiduel, la variable dont vous voulez tracer le résiduel à chaque fois. Sinon, vous aurez toujours le même tracé, correspondant à un calcul précédent.
2 - Toujours dans la fenêtre Optimisation, appuyez maintenant sur le bouton Sensibilité globale. Notez surtout pour l'instant que les graphes obtenus lorsque l'optimisation est correcte doivent avoir la forme de "fonds de paraboles" comme sur la figure suivante :
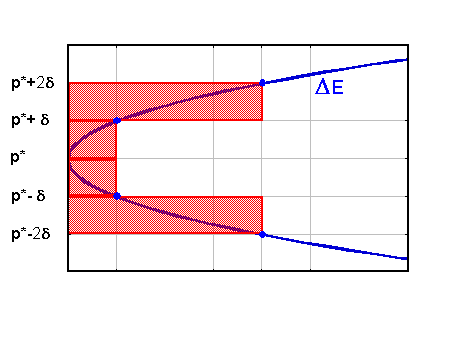
Fig. 3 Diagramme de sensibilité des paramètres.
- p* désigne la valeur courante (ajustée en général) d'un paramètre. Il lui
correspond une erreur résiduelle E*.
Si on fait varier ce paramètre de part et d'autre de sa valeur, en maintenant
les autres paramètres constants, l'erreur résiduelle E varie également, ainsi
que ΔE = E − E*, et on peut montrer qu'au voisinage immédiat d'un
minimum (local ou global), la fonction ΔE = f(p) peut être approximée par
une parabole. Une parabole très "pointue" caractérise un paramètre très
sensible : une très faible variation entraîne une forte variation de l'erreur,
et on peut donc, en général, considérer qu'il est déterminé avec précision.
Inversement, une parabole très "plate" caractérise un paramètre peu sensible,
et par conséquent moins bien déterminé.
La fenêtre Sensibilité globale affiche les barres rouges du diagramme
ci-dessus, correspondant aux valeurs p*±δ et p*±2δ, pour tous les
paramètres ajustables. Il est possible de changer la valeur de δ. Si la
courbe est quasi-parabolique, on obtient donc deux barres centrales à environ
un quart des barres latérales.
Des diagrammes très dissymétriques, ou, à plus forte raison, présentant des
ΔE négatifs sont le signe d'un défaut de l'optimisation : les paramètres
en question ne sont pas à leur position optimale.
L'utilisation de cet outil est plus délicate et demande un peu d'expérience (voir la documentation associée pour une description plus complète). De plus, il s'agit d'une analyse très imparfaite puisqu'elle n'étudie la sensibilté d'un paramètre que dans la situation où les autres sont fixés. La véritable analyse de sensibilité prendrait en compte toutes les interactions des paramètres entre eux et avec les variables, et serait une opération considérablement plus complexe et lourde.
Ce fichier est analogue aux deux précédents, mais avec, cette fois, 10% de bruit ajouté. Cela correspond, seulement du point de vue du bruit, à des données de qualité relativement médiocre, mais c'est très souvent le cas.
Dans cette situation, l'estimation manuelle des paramètres devient beaucoup plus subjective, et moins précise, comme le suggère la figure 4, à comparer avec la figure 1, mais ce n'est pas très gênant pour démarrer une optimisation.
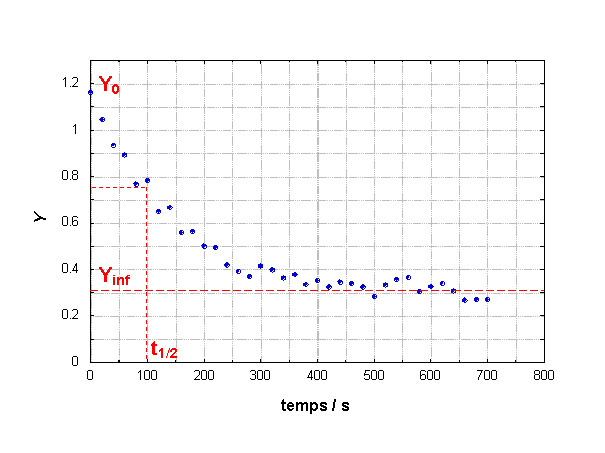
Noter, en particulier, que la valeur initiale est elle-même bruitée. On peut
lire ainsi, maintenant, Y0 ≈ 1.16.
Deux possibilités se présentent alors :
- si la valeur initiale est en fait connue précisément, de manière
indépendante, ce qui est effectivement le cas ici (Y0 = 1.2), il convient d'utiliser cette valeur et
de la considérer comme non-ajustable
- sinon, il est préférable de la laisser ajuster.
A - Maintenez, en un premier temps, Y0 = 1.2 non-ajustable, choisissez des valeurs de départ pour k et Y∞, et lancez une optimisation.
A la question " Estimation automatique de l'erreur ? ", répondez Oui cette fois : la fenêtre Lissage Dérivation (écran 6) s'ouvre, pré-programmée pour le lissage seul.
Vous pouvez garder les paramètres de lissage par défaut (Degré = 3 ; Fenêtre glissante = 13), ou les modifier à l'aide du curseur correspondant (Degré = 2 ; Fenêtre glissante = 9 par exemple, seraient mieux adaptés au nombre total de points, 36 dans ce cas). Voir la rubrique de l'aide Lissage / Dérivation, ou le chapitre VIII du Manuel (p.47), pour une explication plus détaillée de cette fonction et de ces paramètres. Cette fonction peut être utilisée également en dehors de tout ajustement (bouton Lisser / Dériver de l'onglet Données exp.)
Ecran 6. Fenêtre Lissage,
Dérivation.
Appuyer sur le bouton Calculer.
Cela effectue un lissage de la courbe expérimentale et calcule l'erreur résiduelle, à partir de l'écart entre celle-ci et la courbe lissée. Ces deux courbes sont tracées dans une page graphique, et l'estimation de l'erreur résiduelle que l'on peut attendre est proposée dans une fenêtre (écran 7).
Ecran 7.
Vous pouvez adopter cette valeur à la place de sa valeur actuelle en cliquant 2 fois dessus.
Noter que l'erreur résiduelle après ajustement sera toujours un peu supérieure à l'estimation ci-dessus. En effet, comme vous pouvez le voir sur le tracé, la courbe lissée a tendance à suivre légèrement le bruit, et donc à diminuer l'écart entre les deux courbes.
Présence d'un bug dans le module graphique. Si aucun tracé n'a été préalablement effectué, le tracé effectué automatiquement après le lissage provoquera une erreur dont le message est totalement incompréhensible (" n'est pas une valeur en virgule flottante correcte) et qui empêchera l'estimation du résiduel. Veillez donc à toujours effectuer un premier tracé, par exemple par une simple simulation.
Achevez l'optimisation.
Vous devez obtenir une erreur résiduelle autour de 8×10−4, à comparer aux 5×10−4 estimés (écran 7).
L'ajustement de la constante de vitesse doit donner k ≈ 7.4×10−3 s−1, soit une valeur légèrement supérieure à celle qui a servi à générer les données expérimentales.
B - Recommencez une optimisation, avec les mêmes paramètres de départ, mais en marquant cette fois Y0 ajustable.
Dispensez-vous de l'estimation de l'erreur, qui sera évidemment la même.
L'erreur résiduelle doit être légèrement plus faible que lorsque Y0 était maintenu fixe. C'est normal puisqu'on donne maintenant un degré de liberté supplémentaire.
Quant à la constante de vitesse ajustée, elle doit être maintenant k ≈ 7×10−3 s−1, soit une valeur légèrement inférieure à celle qui a servi à générer les données expérimentales, contrairement au cas précédent. Cette différence en sens opposé est fortuite et on obtiendrait des résultats différents avec un bruit différent (ou une expérience réelle différente), mais cela montre clairement que le résultat d'une optimisation dépend de la façon dont elle est menée, particulièrement du nombre de paramètres ajustés, et cela d'autant plus que le niveau de bruit est important.
Cette petite expérience donne également une idée de la précision que l'on peut attendre sur les paramètres ajustés. Ainsi, par exemple, l'optimisation B conduit à une constante de vitesse diffférente de l'optimisation A de 0.4/7, soit environ 6%.
Il n'en reste pas moins que la présence de bruit dans les données expérimentales, même à un niveau relativement élevé, n'empêche pas forcément un ajustement correct et significatif. Deux conditions doivent être satisfaites cependant :
1- il doit s'agir réellement de bruit, aléatoire, et non d'un biais. Cela n'est pas toujours aisé à réaliser ou à prouver, mais on doit en tout cas préférer les données expérimentales les plus brutes possibles, ne jamais leur substituer un pré-traitement, qui risquerait justement de les biaiser.
Par exemple, il est tout à fait à proscrire d'effectuer un lissage préliminaire des données expérimentales : cela ne peut qu'introduire un biais supplémentaire. Il faut se méfier, d'autre part, de certains logiciels intégrés sur les appareils de mesure qui transforment les données brutes, directement en concentrations, par exemple.
2- plus le niveau de bruit est important, plus le nombre de points doit être grand. Les 36 points que nous avons utilisés ici représentent clairement un minimum.
Vous pouvez essayer cette fois, puisqu'il y a maintenant trois paramètres ajustables, de brouiller leur ordre initial. Revenez pour cela aux paramètres de départ adoptés ci-dessus. Relancez une optimisation. Appuyez sur le bouton Brouiller de la fenêtre Ordre des directions initiales. Assurez-vousque l'ordre a bien été modifié. Appuyez de nouveau si ce n'est pas le cas (lorsque le nombre de paramètres est petit, la probabilité de retrouver le même ordre est élevée).
Vous devez obtenir, dans le cas présent, des résultats très proches des précédents, bien que légèrement différents. Cela confirme simplement ici que deux chemins d'optimisation différents conduisent au même minimum. Il est vivement conseillé de vérifier qu'il en est également de même avec des paramètres de départ différents (mais réalistes). Ces vérifications sont d'autant plus nécessaires que le nombre de paramètres est important. D'autre part, brouillage de l'ordre initial et variation des valeurs de départ sont quelquefois suffisants pour sortir d'un minimum local.
Nous allons maintenant tester le modèle (expon.cpp) sur des jeux de données complètement différents. Il s'agit en réalité de données ressemblant beaucoup aux précédentes, mais correspondant à une réaction bimoléculaire, avec un niveau de bruit de 2 et 10%.
Télécharger non_expon_2pc.exp Télécharger non_expon_10pc.exp
A - Ajustez les deux paramètres, k et Y∞, sur l'expérience non_expon_2pc.exp.
Vous devez trouver des valeurs proches des précédentes, y compris pour l'erreur résiduelle. Le graphique montre cependant que la courbe ajustée ne passe pas vraiment dans les points expérimentaux, ce que confirme nettement le tracé des résiduels. On peut en conclure que le modèle exponentiel ne convient pas pour ces données, et que, par conséquent, les paramètres ajustés n'ont pas de signification réelle.
B - Ajustez de même k et Y∞ sur non_expon_10pc.exp.
Vous retrouvez encore des valeurs assez proches. Par contre, il est impossible de dire à la seule vue de la courbe ajustée et des points expérimentaux si l'ajustement peut être considéré comme correct. Le tracé des résiduels, lui, présente la même allure générale de concavité vers le bas que dans le cas précédent, mais de manière beaucoup moins nette. De sorte qu'il serait difficile de décider uniquement avec cela si le modèle exponentiel convient ou non dans ce cas. Faute d'expériences complémentaires, ou plus précises, on serait tenté d'accepter le modèle.