complément

Réaction bimoléculaire réversible : A + B ⇄ C + D     k₀, k₁     (r 10)

forme des courbes cinétiques en fonction du sens de la relaxation

On suppose k₀ > k₁.

Réécrivons l'équation

dE/dt  =  −[ k₀ (B_e+A_e) + k₁ (C_e+D_e) ] E  +  (k₁−k₀) E²     (51)

ou  dE/dt  =  p E  +  q E²

 

 en termes de vitesse et d'avancement normalisés :

r_norm  =  r / r_initial  =  (dE/dt) / (dE/dt)|_{t = 0}

χ  =  (E₀−E) / E₀    d'où    E  =  E₀ (1−χ)

r_norm  est une grandeur positive, variant de 1 à 0 quand χ varie de 0 à 1.

Il vient :

r_norm  =  (pE + qE²) / (pE₀ + qE₀²)

r_norm  =  [pE₀(1−χ) + qE₀²(1−χ)²] / (pE₀ + qE₀²)

et finalement :

r_norm  =  (1−χ) [1−qE₀χ / (p + qE₀)]

soit

r_norm  =  (1−χ) (1−α χ)     (a)

avec

α  =  qE₀ / (p + qE₀)

Afin de discuter le signe de α, il faut remarquer que si l'écart à l'équilibre E, tel qu'on l'a défini (49), peut être positif (A₀>A_e), ou négatif (A₀<A_e), E/E₀ est nécessairement toujours positif, et (dE/dt)/E₀ nécessairement négatif, sinon cela voudrait dire que la réaction s'écarte de l'équilibre. Or :

(dE/dt)|_{t = 0} / E₀  =  p + qE₀

on a donc

p + qE₀  <  0     ∀ E₀

q étant négatif également (k₀ > k₁), le signe de α est donc égal à celui de E₀.

Le premier terme de l'équation (a) représente la vitesse normalisée de l'ordre 1 (courbe en pointillés gris sur la figure). Le deuxième terme correspond à une droite d'ordonnée à l'origine égale à 1 et de pente −α.

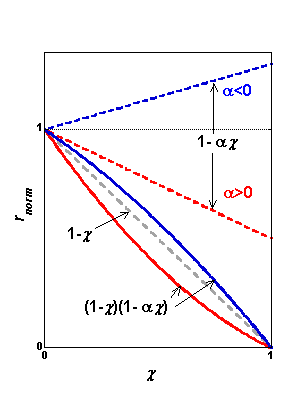
Ainsi, lorsque E₀ est positif, (1−χ) est multiplié par un facteur toujours inférieur à 1 et on a (droite et courbe en rouge) :

r_norm  <  (1−χ)

et, inversement, lorsque E₀ est négatif, (1−χ) est multiplié par un facteur toujours supérieur à 1 et on a (droite et courbe en bleu) :

r_norm  >  (1−χ)

Ce dernier cas correspond à la situation où, bien que l'équilibre soit en faveur du couple C-D (k₀ > k₁), la réaction démarre avec un excès de C et D et se déroule donc en sens inverse de la flèche principale.